Cool stuff in NIPS 2015 (workshop) - Non-convex optimization in machine learning

“When I am a grown-up I want to do non-convex optimization”. This blog post is about NIPS 2015 workshop of non-convex optimization in machine learning and some interesting papers on non-convex optimization appeared in the NIPS conference.

Table of content

Invited talk on Recent advances and challenges in non-convex optimization

Short summary

  1. This invited talk is mostly about approaching some non-convex optimization problem via tensor decomposition or tensor algebra.
  2. As many real-world big-data optimization problem are statistically and computationally hard for which
    1. we need large number of examples in order to estimate the model.
    2. we need to tackle the non-convexity in order to achieve computational feasibility.
  3. For example, solving these problem with stochastic gradient descent (SGD) with multiple random initialization will generally give very poor results due to multiple local optimals.
  4. On the other hand, some of these hard optimization problems can be formulated as the tensor decomposition or via tensor algebra.
  5. Then there are two strong claims about this tensor decomposition:
    1. Though most tensor decomposition problems are also non-convex and NP-hard, running SGD will provide some satisfactory optimization results.
    2. We can converge to global optimal solution despite we have a non-convex optimization problem via tensor decomposition.
  6. Theses two claims from the speaker are quite strong, it might be worthwhile to check the original publications.
  7. Keywords of the talk might be e.g., tensor decomposition, non-convex optimization, spectral optimization, robust PCA.

Introduction

  1. Learning is like finding needle in a haystack.
    1. Big data is challenging due to large number of variables and high-dimensionalities.
    2. Useful information is essentially represented as some low-dimensional structure.
    3. Problem when learning with big data:
      1. Statistically: large number of examples are needed in order to estimate the model.
      2. Computationally: mainly about non-convexity, a lot of SGD restarts are required to avoid local optimals and to reach global optimal.
    4. Algorithm should scale both to the number of samples and variables.
  2. Optimization for learning
    1. Unsupervised learning: maximize similarity of cluster, maximize likelihood of model.
    2. Supervised learning: minimize some cost function.
    3. Most of them are non-convex optimization problem.
    4. A Facebook page for non-convex optimization.
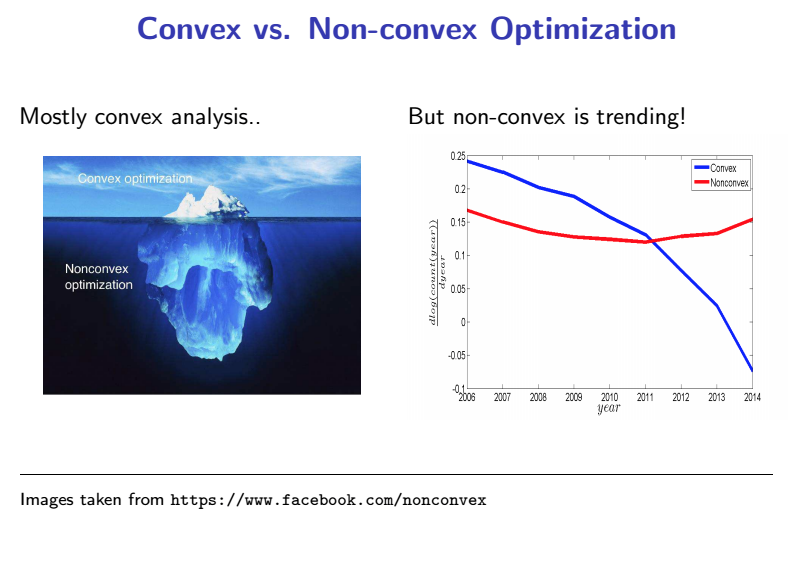
    5. Convex has a unique global optimal solution, SGD will lead to the unique global optimal.
    6. Non-convex has multiple local optimal, possibly exponential local optimals in high dimensional space. This makes large scale learning challenging.

  3. Non-convex optimization is a trending research area compare to convex optimization.

    photo1

  4. Non-convex optimization and Curse of dimensionality
    1. Difficulty in non-convex optimization: multiple optimalities exist.
    2. Curse of dimensionality is the concept we all come across during the introductory course of machine learning but easily forget afterwords. As a short summary, it actually means
      1. The volume of the space increases very quickly when the dimensionality increases such that available data become very sparse.
      2. In order to have statistical significancy, the number of data points required to support the results in the space will grow exponentially with the dimensionality.
      3. High-dimensionality might not always be good, we frequently use dimensionality reduction techniques, e.g., principal component analysis (PCA) to reduce dimension while keeping the similar amount of useful information.
    3. I still need to find out the relation of curse of dimensionality and anomaly detection.
    4. In optimization, curse of dimensionality means exponential number of crucial points (saddle points of which the gradient is zero).
  5. Method in one sentence: model the optimization problem with tensor algebra, run SGD for non-convex tensor decomposition problems.

Methods

  1. Take data as a tensor object
    1. Matrix view: pairwise correlation.
    2. Tensor view: high order correlation.
  2. Spectral decomposition
    1. Look at matrix decomposition and tensor decomposition
      1. Matrix decomposition: \(M_2 = \sum_{i=1}^{r}\lambda_i u_i\otimes v_i\).
      2. Tensor decomposition: \(M_3 = \sum_{i=1}^{r}\lambda_i u_i\otimes v_i \otimes w_i\).
      3. This is the problem under study here in this talk. The goal is to solve this efficiently and with some good result in term of optimization quality. Essentially, they are non-convex optimization problem.
    2. Singular value decomposition (SVD)
      1. SVD of a 2D matrix can be formulate as the following convex optimization problem (calculating the first eigen-value) \(\underset{v}{\max}\,<v,Mv>\, \text{s.t.}\, ||v||=1,v\in\mathbb{R}^d\).
      2. With all eigen-values computed, SVD can be seen as, e.g., decomposing a document-word matrix into a document-topic matrix, a topic strength matrix, and a topic-word matrix.
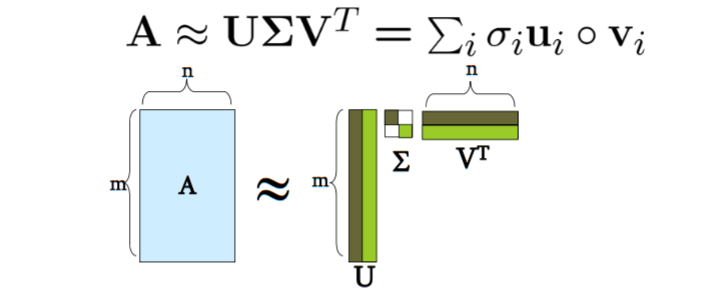
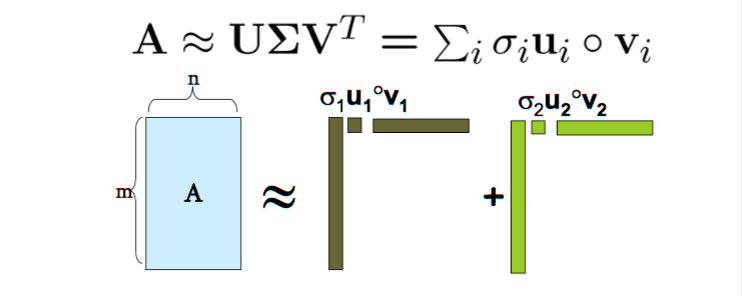
    3. SVD and tensor decomposition photo1 photo1
    4. Principal component analysis (PCA) is an important application of SVD which finds new axises of a data cloud that explains the variance in the data.
    5. Tucker decomposition:
      1. Given an input tensor as a \(I\times J\times K\) matrix \(X\), decompose it into a \(I\times R\) matrix \(A\), a \(J\times S\) matrix \(B\), a \(K\times T\) matrix \(C\), and a \(R\times S \times T\) diagonal matrix \(G\).
      2. This is a non-convex problem and can be solved approximately by alternating least square (ALS).
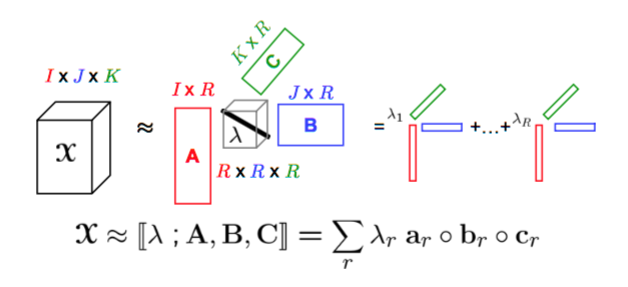
    6. Canonical decomposition (CANDECOMP) or Parallel factor (PARAFAC): photo1
      1. Given an input tensor as a \(I\times J\times K\) matrix \(X\), decompose it into a \(I\times R\) matrix \(A\), a \(J\times R\) matrix \(B\), a \(K\times R\) matrix \(C\), and a \(R\times R \times R\) diagonal matrix \(G\).
      2. This is almost the same as Tucker decomposition. It is a non-convex problem and is solved by ALS.
    7. Robust tensor decomposition: given an input tensor (3D matrix) \(T=L+S\), we aim to recover both \(L\) and \(S\), where \(L\) is a rank \(r\) orthogonal tensor and \(S\) is a sparse tensor. In particular, \(L\) has the form \(L = \sum_{i=1}^{r}\delta_iu_i\otimes u_i \otimes u_i\). This is non-convex optimization problem.
    8. Robust PCA: is the same as tensor decomposition but in a matrix form. This can be formulated either as a convex or non-convex optimization problem.
  3. The talk suggests two algorithm for tensor decomposition:
    1. One for orthogonal tensor decomposition problem.
    2. The other for non-orthogonal tensor decomposition problem.

Implementation and applications

  1. A list of implementation is also provided as in the slides, which also includes this spark implementation. Need to checkout the performance. In this paper they mentioned that the underlying optimization algorithm is embarrassingly parallel. So looks promising :question:

  2. Other interesting tensor decomposition: dynamic tensor decomposition, streaming tensor decomposition, and window based tensor analysis.

  3. Applications of tensor analysis

    1. Unsupervised learning: GMM, HMM, ICA, topic model (not very clear).
    2. Training deep neural network, back-propagation has highly non-convex loss surface, tensor training has better loss surface.
    3. Sensor network analysis as a location-type-time tensor.
    4. Social network analysis as a author-keyword-time tensor.

Other information

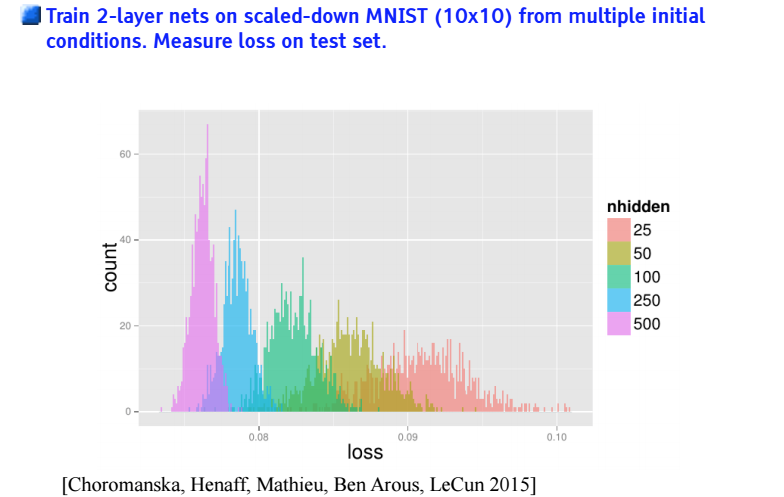
  1. Loss function in deep neural network looks like random Gaussian polynomial.
    1. The main result is that all local minimals have similar values.
    2. Exponential number of saddle points which is difficult to escape.
  2. To avoid saddle points
    1. Use second order information: Hessian matrix.
    2. Use noisy stochastic gradient.
    3. Compute a convex envelop.
    4. Smooth out the non-convex function.

Additional materials

  1. Slide for the talk.

  2. Two related papers from her research group that appears in this workshop
    1. Convolutional dictionary learning through tensor factorization
    2. Tensor vs matrix methods: robust tensor decomposition under block sparse perturbations
  3. She also gave some similar talks about non-convex optimization and tensor decomposition
    1. Tensor methods for training neural networks.
    2. Beating the perils of non-convexity machine learning using tensor methods.
    3. Tensor methods: a new paradigm for training probabilistic models and for feature learning.
  4. Other interesting materials about tensor decomposition
    1. Quora: Open problems in tensor decomposition.
    2. Paper: Most tensor problems are NP-hard. Quoted from this paper ’ “Bernd Sturmfels once made the remark to us that “All interesting problems are NP-hard.” In light of this, we would like to view our article as evidence that most tensor problems are interesting.”‘
    3. Tutorial: Mining Large Time-evolving Data Using Matrix and Tensor Tools .

Invited talk on Large-scale optimization for deep learning

There is a very interesting point in this talk: it is relatively easier to optimize a very large neural network on a small machine learning problem.

photo1

Hongyu Su 26 December 2015