NIPS conference 2015

Some experience in NIPS2015 conference.

Table of content

NIPS 2015

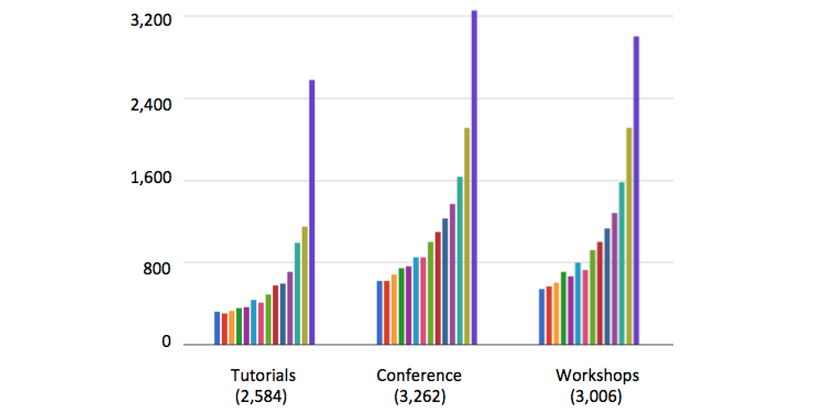
  1. There seems to be an exponential growth for NIPS participants as shown in the following picture. It is said that about 10% papers are from deep learning and roughly 5% from convex optimization. photo1

  2. One big news in NIPS is that Elon Musk plan to commit 1 billion dollars to create a non-profit research organization known as OpenAI. See also the press release of the New York Times. OpenAI will base in San Fransisco with a long term goal is to create an artificial general intelligence (AGI) that is capable of performing intellectual task as human beings. The funding for openAI is extremely high which makes people curious about what they are going to achieve after a few years.

    photo1

    A researcher from OpenAI claims that the research will mostly be driven by empirical results rather than theory as they think in the field of neural network the empirical achievement is way ahead of the theory at the moment. At the same time, they don’t restrict themselves on deep stuffs.

  3. A research startup the CurousAI company based in Helsinki with partners from Aalto university and Nvidia. They have a paper in NIPS conference semi-supervised learning with ladder networks and a 300m presentation.

    photo1

    Obviously, they only do stuffs in deep neural network.

  4. My personal comment on these deep companies: I think deep learning involves more engineering work than scientific research. There is no problem for big company like Google and Facebook to invest money and brains for the purpose of making more money. Look at the funding member of both AI research companies, they are all deep learning people. AI or AGI are believed to be far more complicated than engineering. And I think deep learning is very premature to be a working horse of creating an AI or AGI. But throwing money to research is always a good sign :laughing:

Workshops

  1. Non-convex optimization in machine learning

  2. Time series

  3. Optimization

Symposiums

  1. Algorithm among us

  2. Neural style

Interesting conference papers

Non-convex optimization

In general, non-convex optimization problems are NP-hard. One fundamental direction for non-convex optimization research is to extend the class of functions that one can solve efficiently

  1. Beyond convexity: stochastic quasi-convex optimization
    1. Convex Lipschitz functions can be minimized efficiently using stochastic gradient descent (SGD).
    2. Propose a stochastic version of Normalized gradient descent (NGD) and prove the convergence for a wide class of functions
      1. Quasi-convex
      2. Locally-Lipschitz

Another interesting direction on non-convex optimization is to develop efficient polynomial time algorithm for some specific optimization problems under some reasonable assumptions.

  1. Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems

    1. Video of the 20 mins oral presentation.

    2. The problem is finding a solution \(x\) to a quadratic system of equations (non-linear)

      \(y_i = <a_i,x>^2,\quad i=1,\cdots, m\).

    3. It is a non-convex optimization problem.
    4. Solving the quadratic system of equation is to find rank one solution based on a collection of linear constraints 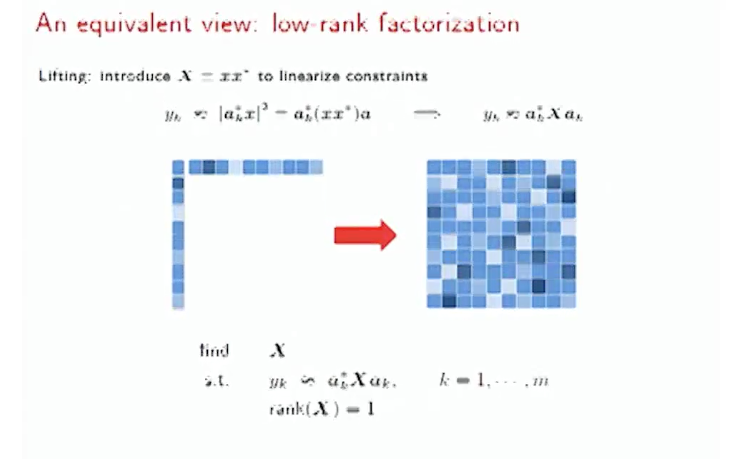photo1 Therefore, it is similar as low rank matrix estimation.
    5. The paper is saying that a quadratic system equations with \(n\) variables can be solved in \(\Theta(n)\).
    6. The key ingredients:
      1. Assumption:
        1. Unstructured random system \(A\) is a random matrix i.i.d.
        2. This is not very strong, can be well beyond i.i.d. model, as long as there is some non-coherence information.
      2. Stage 1: regularized spectral intialization procedure.
      3. Stage 2: regularized iterative descend procedure :question: geometric convergent rate.
    7. Basically, the gradient descent with spectral initialization can work in non-convex optimization problem. Evidence can also be found from this paper A nonconvex optimization framework for low rank matrix estimation
    8. Empirically, the speed of the proposed algorithm solving quadratic system of equations is about four times of solving a least square problem of the same size.
  2. A Nonconvex Optimization Framework for Low Rank Matrix Estimation
    1. The problem under study is low rank matrix estimation via non-convex optimization.
    2. Compared to convex relaxation, non-convex approach has superior empirical performance (this claim comes from this paper).
    3. Propose an optimization algorithm called projected oracle divergence.
    4. Prove the convergence to global optima for e.g., alternating optimization and gradient-type method for non-convex low rank matrix estimation.
    5. The optimization algorithm has geometric convergence rate.
  3. A Convergent Gradient Descent Algorithm for Rank Minimization and Semidefinite Programming from Random Linear Measurements

    1. A simple, scalable, and fast gradient descent algorithm for non-convex optimization of affine rank minimization problem.

      \[\underset{X\in R^{n\times p}}{\min}rank(X), \quad \text{subject to}\, A(X)=b\]
    2. The rank minimization problem can be written as a particular class of SDP problem, the proposed method offer a fast solution for SDP compare to interior point methods.
    3. The key ingredient is that the low rank minmization problem is conditioned on the transformation \(A:R^{n\times p}\rightarrow R^m\).
    4. The proposed gradient algorithm has a Linear convergence rate.

Convex optimization

Others

  1. Data science in the next 50 years
Hongyu Su 16 December 2015